Проект урока математики Применение производной для исследования функций" 10«Б» кл. Степырева Любовь Ивановна – высшая квалификационная категория, учитель МОУ "СОШ № 7" г. Коряжма

Тема :Применение производной для исследования функций.
Характеристика класса:
В группах физико-математического и физико-химического профилей занимаются все учащиеся класса. Класс сформирован по желанию учащихся и их родителей без предварительного отбора. Курс математики изучается по учебнику «Алгебра и начала анализа» под редакцией А.Г.Мордковича. Дополнительно используется задачник профильного уровня. Курс геометрии изучается по учебнику «Геометрия 10-11 классы» Л.С. Атанасян и др.
Высокий уровень сформированности ОУУН имеют 9 человек, средний-9 человек, низкий-6 человек. Урок проводится на этапе окончания изучения темы «Производная и ее применение». Тема раскрывает способы применения дифференцирования при решении задач по математике и физике и тем самым расширяет объем знаний учащихся по физике и началам анализа, формирует у них убеждение в связности предметов, в целостности мира, совершенствует подготовку старшеклассников к ЕГЭ.
Цели:
1.Создание условий для формирования научного мировоззрения посредством использования методов математического анализа.
2.Развитие логического мышления через использование знаний смежных наук.
3.Развитие коммуникативных умений.
Тип урока: урок применения знаний, умений и навыков.
Структура урока:
1. Мотивация учебной деятельности.
2. Актуализация опорных знаний.
3. Работа в парах
4. Совместная деятельность учащихся и учителя по решению задач.
5. Рефлексия
6. Домашнее задание.
Формы организации познавательной деятельности:
1. Общеклассная.
2. Индивидуальная
3. Парная.
Метод обучения: частично-поисковый.
Средства обучения: дидактический материал.
Прогнозируемый результат: учащиеся должны научиться применять полученные теоретические знания для решения практических задач, в том числе по смежным дисциплинам.
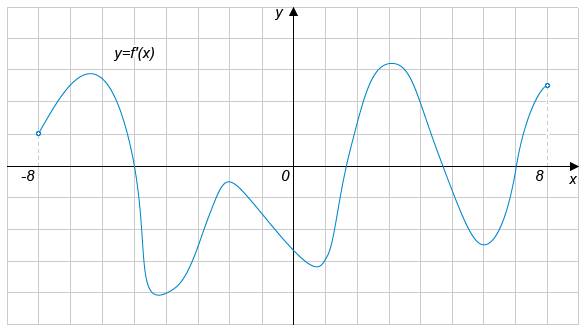
Математический диктант
|
1 вариант |
2 вариант |
|
1.Определите количество промежутков возрастания функции y=f(x) на (-8; 8). |
1.Определите количество промежутков убывания функции y=f(x) на (-8;8). |
|
2.Определите количество точек экстремума на заданном промежутке. |
2.Определите количество точек, в которых касательная к графику функции y=f(x) параллельна оси ох. |
|
3. Определите количество точек, в которых касательная к графику функции y=f(x) образует с положительным направлением оси ох угол 600. |
3. Определите количество точек, в которых касательная к графику функции y=f(x) образует с положительным направлением оси ох угол 300. |
|
4. Определите количество точек, в которых касательная к графику функции y=f(x) параллельна прямой у=3х+2 или совпадает с ней. |
4. Определите количество точек, в которых касательная к графику функции y=f(x) параллельна прямой у= -3х+2 или совпадает с ней. |
|
5. Материальная точка проходит расстояние S ( в метрах), которое определяется по закону S(t)=t2-2t. Какой будет скорость точки через 4 секунды после начала движения? |
5. Материальная точка проходит расстояние S ( в метрах), которое определяется по закону S(t)=t2-12t+35. Через какое время после начала движения точка остановится? |
Карточка № 1.
На рисунке изображен график производной функции у=f(x), определенной на интервале (-8;3).
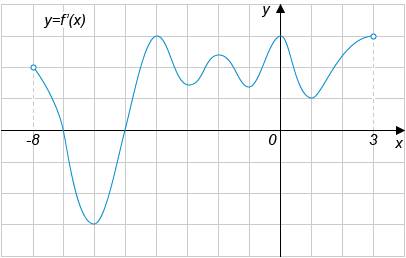
1. Найдите промежутки убывания этой функции.
2. Найдите количество точек экстремума функции у=f(x).
3. Найдите количество точек, в которых касательная к графику функции y=f(x)параллельна прямой у=2х+16, или совпадает с ней.
4. Найдите количество точек графика функции y=f(x), в которых касательная составляет с положительным направлением оси абсцисс угол в 450.
5. В какой точке интервала (-6;3) функция y=f(x) принимает наименьшее значение.
Карточка №2.
На рисунке изображен график функции y=f(x), определенной на интервале
(-4;10)
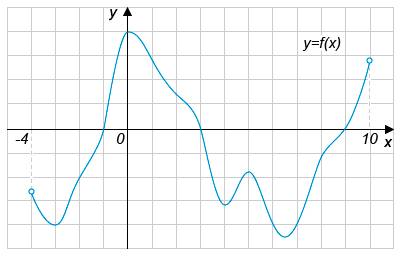
1. Найдите промежутки убывания этой функции на интервале (-4;10)
2. Определите количество точек экстремума на указанном интервале.
3. В какой точке интервала функция принимает наибольшее значение?
4. На каких интервалах производная этой функции отрицательна?
5. Определите количество точек графика функции y=f(x), в которых касательная к графику функции параллельна оси абсцисс.
Карточка №3.
1.Материальная точка движется прямолинейно по закону X(t)=- t3+t2+5t-29,( где х – расстояние от точки отсчета в метрах, t- время в секундах, измеренное с начала движения.)
а)Найдите скорость материальной точки в момент времени t=2 секунды.
б)В какой момент времени материальная точка остановится?
в)В какой момент времени материальная точка имела наибольшую скорость? Каково было ее ускорение в этот момент?


